고정 헤더 영역
상세 컨텐츠
본문
글을 쓰기전 이 글의 모든 내용은 다크 프로그래머님의 영상 Geometry 포스팅을 읽고서 요약 정리한 것임. 글에 나와있는 사진과 내용의 모든 저작권은 다크프로그래머님에게 있음.
다크 프로그래머 :: 다크 프로그래머 (tistory.com)
다크 프로그래머
영상처리 & 프로그래밍
darkpgmr.tistory.com
영상 Geometry #5. 3D 변환
1. 3D 변환
컴퓨터 비전에서 관심있는 3D 변환은 회전과 평행이동 뿐임. 갑자기 커지거나, 모양을 변화하는 건 관심 없음.
2. 변환행렬

3차원 공간의 점 (x, y, z)를 x, y, z 축 중심으로 세타 회전시키는 변환행렬은 위와 같음. 회전방향은 반시계 방향임. 참고로 임의의 단위벡터 u를 회전축으로 회전시키는 변환행렬 공식도 존재함.

3개의 기본 회전변환을 조합하면 위와 같이 임의의 3D 회전을 표현가능.

회전변환에 평행이동까지 포함하면, 위와 같은 일반적인 3D변환식이 완성됨.

2D 변환과 마찬가지로, 3D변환에서도 homogeneous 좌표를 이용하면, 회전변환과 평행이동을 하나의 변환행렬(Rigid 변환)으로 표현가능함.
3. 회전변환 구하는 법
크기가 같은 임의의 두 벡터가 있을 경우, 다음과 같은 순서로 둘 사이의 회전변환을 유도할 수 있다.
먼저, 회전각도인 두 벡터 사이의 사잇각은 내적을 통해 알아낸다. 다음으로 회전축을 알아야 하는데, 이는 두 벡터의 외적을 통해 구할 수 있다. 이렇게 축과 회전각도를 알면, 앞서 언급한 공식을 통해 회전변환행렬을 구할 수 있다.
4. 회전변환 + 평행이동 구하는 법
3D 변환에서 Rigid 변환을 위해 필요한 매칭쌍의 개수는 3개임. 다크그래머님의 포스팅의 예시를 들면,
다음과 그림과 같이 주어진 3개의 매칭쌍 p1-p1', p2-p2', p3-p3'를 이용하여 A에서 A'로의 rigid 변환관계를 구한다고 할때,
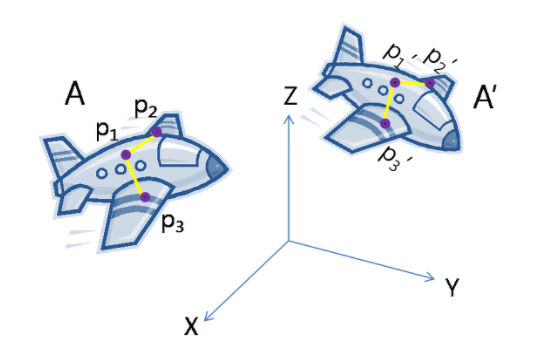
1) p1이 원점이 되도록 A를 평행이동 시킨 후, 2) A'의 방향과 일치되도록 회전시켜서, 3) p1'까지 평행이동시키는 방법을 통해 구할 수 있다고 한다.
5. 좌표축 변환 (월드 좌표계 -> 카메라 좌표계)
월드좌표계 상에서 카메라 초점(카메라 좌표계의 원점)의 좌표를 (Fx, Fy, Fz), 월드좌표계의 좌표축을 카메라 좌표계 좌표축으로 회전시키는 행렬을 R이라 하자.

월드좌표계 상 점 (X, Y, Z) 를 카메라 좌표계로 봤을 때의 좌표 (Xc, Yc, Zc)로 위와 같은 과정을 통해 변환할 수 있다. 여기서 R의 역행렬을 사용하게 되는데, R의 전치행렬과 그 값이 같다.
영상 Geometry #6. 이미지 투영
3D 월드좌표에서 2D 픽셀좌표으로의 변환관계를 살펴보자.
1. 원근 투영변환
(여기서 이미지 평면상의 원점은 이미지 평면의 왼쪽 상단이 아니라, 이미지 평면과 광학축 Zc와의 교점,)
원근 투영변환이란 3D 상의 점을 이미지 평면에 투영하는 변환으로, 다음 그림을 통해 쉽게 이해할 수 있다. f는 초점거리로써, 렌즈중심과 이미지 센서와의 거리를 뜻함.

투영기준점을 어디에 잡냐에 따라 두가지 경우로 나눌 수 있다. 첫번째 경우는, 투영 기준점을 카메라 좌표계의 원점으로 잡고, 이미지 평면을 Zc = d에 두는 경우이다. 이때, 3D 상의 점(Xc, Yc, Zc)과 투영된 이미지 평면 상의 점(u, v, 1) 사이에는 다음과 같은 관계가 성립한다. (여기서 s는 homogeneous 좌표표현의 scale factor임. 크게 중요 X)

즉, 투영평면이 Zc = d일 경우 (Xc, Yc, Zc, 1)는 (Xc, Yc, Zc/d) = (d*Xc/Zc, d*Yc/Zc, 1)로 투영. 두번째 경우는, 투영 기준점을 (0, 0, -d) 로 잡고, 이미지 평면을 Zc = d에 잡는 경우로 다음과 같은 관계가 성립한다.
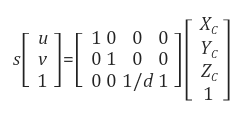
이외에도 투영변환을 표현할 수 있는 방법은 다양하지만, 여기서는 첫번째 경우를 기준으로 설명.

2. 이미지 투영 모델
이제 월드 좌표계 상의 점 (X, Y, Z)를 이미지 평면(픽셀 좌표계) 상의 (x, y)로 변환하는 과정을 살펴보자.

이해를 돕기위해 설명하면 [R|t]는 좌표계 변환행렬로써, 영상 Geometry #5의 마지막 부분에서 설명한 월드좌표계를 카메라 좌표계로 바꾸는 Rigid 변환 행렬이다. Tpers(1)은 Zc = 1(d=1) 로의 투영변환, 즉 카메라 좌표계 상의 3D 좌표를 정규 이미지평면에 투영시키는 행렬이다. 그리고 K는 카메라 내부(intrinsic) 파라미터 행렬로 정규 이미지 좌표를 픽셀 좌표로 바꿔주는 행렬이다. (6) 식은 (5)식을 풀어서 쓴 식이라 생각하면 된다.
여기서 투영변환과 [R|t]를 합쳐서 표현하면 아래와 같이 더 간단하게 정리 될 수 있다.

[R|t]를 카메라 외부 파라미터(extrinsic parameter), K를 내부 파라미터(intrinsic parameter)라고 부른다. 그리고 K와 [R|t]를 합쳐서 camera matrix 또는 projection matrix라 부름.
영상 Geometry #7. Epipolar Geometry
Epipolar geometry는 스테레오 비전(stereo vision) 즉, 2-view 비전에서의 기하라고 생각하면 된다.

가령 위와 같은 그림이 있을때, Epipolar geometry는 동일한 사물 또는 장면에 대한 영상을 서로 다른 두 지점에서 획득했을 때, 영상 A와 영상 B의 매칭쌍들 사이의 기하학적 관계를 다루는 것임.
1. 용어 및 기본개념
그림1 과 같이 3차원 공간상의 한 점 P가 영상 A에서는 p에 투영되고, 영상 B에서는 p'에 투영됐다고 하자. 이 때, 두 카메라 원점을 잇는 선과 이미지 평면이 만나는 점 e, e'을 epipole 이라 부르고 투영점과 epipole을 잇는 직선 l, l'을 epilin이라 함.
두 카메라 위치 사이의 기하학적 관계 [R|t]를 알고 있고 영상 A에서의 영상좌표 p를 알고 있을 때, 영상 B에서 대응되는 점 p'의 좌표를 구하는 문제를 생각해 보자.
점 P까지의 거리 정보를 모른다면 영상좌표 p로부터 투영되기 전의 3차원 좌표 P를 복원할 수는 없고, 점 P가 영상 B에 투영된 좌표 p' 또한 유일하게 결정할 수 없음.
하지만 점 P는 A 카메라의 원점과 p를 잇는 직선(ray) 상에 존재하기 때문에 이 직선을 영상 B에 투영시키면 점 p'이 이 투영된 직선 위에 있음은 알 수 있습니다. 이 직선이 바로 epiline l' 임.
여기서 한 영상좌표로부터 다른 영상에서의 대응되는 epiline을 계산해주는 변환행렬이 Fundamental Matrix, Essential Matrix 입니다.
2. Essential Matrix

임의의 두 지점에서 찍은 영상의 매칭점들은 항상 식 (1)을 통해 관계지을 수 있으며, 이 때 식 (1)을 epipolar constraint (또는 essential constraint), 이 3×3 행렬 E를 Essential Matrix라 부른다. 주의할 점은 여기서 p'와 p는 정규 이미지 평면위의 점이다.
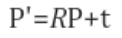
P를 A 카메라 좌표계에서 본 외부 공간의 점의 좌표라 하고, P'을 B 카메라 좌표계에서 본 좌표라 하면 위와 같은 관계가 성립한다. (R은 두 카메라 좌표계 사이의 회전행렬, t는 평행이동)

여기서 Essential Matrix를 위와 같이 잡을 수 있다. [t]xR은 t와 R과의 외적을 의미하는게 아니라 먼저 R로 회전을 시킨 후 다음에 t와 외적을 시키는 일련의 선형변환을 의미함. P', E, P 사이에는 다음과 같은 관계가 성립한다. (Essential Matrix를 직접 넣어서 계산하면 성립함.)
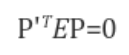
이제 카메라 좌표를 정규 이미지 좌표로 바꾸면, 식(1) (p'Ep=0)을 쉽게 확인할 수 있다.
3. Fundamental Matrix
Essential Matrix는 정규 이미지 평면에서 좌표들 사이의 관계를 설명할 수 있는 Matrix라면, Fundamental Matrix는 카메라 파라미터까지 포함한 두 이미지의 픽셀좌표 사이의 관계까지 설명하는 Matrix임. 더 General하다고 생각할 수 있다.

이 때, 이미지 A에 대한 카메라 내부 파라미터 행렬을 K, 이미지 B에 대한 카메라 행렬을 K', 이미지 A, B 사이의 essential matrix를 E라 하면 fundamental matrix F는 다음과 같이 주어진다.

4. Epipolar Geometry
epipolar geometry에서 다루는 것은 크게 두가지인데 하나는 epipolar constraint이고 다른 하나는 triangulation임.
1) Epipolar constraint
Epipolar constraint는 두 이미지 평면 사이의 기하학적 관계에 따른 constrain으로, 위에서 구한 Essential Matrix로 표현된 관계, p'Ep = 0을 나타낸다.
두 이미지가 주어지고 대응되는 매칭 쌍들을 알고 있을 때, 만일 카메라 파라미터를 모른다면 fundametal matrix F를 직접 구해야 하는데 F를 구하기 위해서는 최소 7쌍의 매칭점들을 필요로 함.
만일 카메라 파라미터를 알고 있다면 Essential matrix E만 구하면 됨. Essential matrix E를 결정하기 위해서는 보통 5쌍의 매칭점을 필요로 하지만, 알고리즘에 따라서는 8 쌍, 3쌍 등 다양함.
2) Triangulation
마지막으로 Triangulation (삼각측량법)은 두 이미지 평면 사이의 기하학적 관계가 주어지고 (즉, E 또는 F가 주어지고), 두 이미지 평면상의 매칭쌍 p, p'이 주어지면 이로부터 원래의 3D 공간좌표 P를 결정할 수 있다는 것을 말함.
'학부 연구생' 카테고리의 다른 글
| [학부 연구생] 처음으로 논문에 이름을 올리다 (0) | 2022.05.06 |
|---|---|
| [학부 연구생] 2022-1 겨울방학 학부연구생 후기 (2) | 2022.03.13 |
| [2022.1.5] 전체 랩세미나 (0) | 2022.01.06 |
| [2022.1.3]연구실 첫 출근 (0) | 2022.01.03 |
| [2021.12.28]김승룡 교수님과 첫 면담 (0) | 2021.12.28 |


댓글 영역